

A line drawn perpendicular to a tangent through the point of contact with a circle passes through the centre of the circle.A line drawn perpendicular to a radius through the end point of the radius lying on the circle is a tangent to the circle.The distance from a point on the circle to a given chord times the diameter of the circle equals the product of the distances from the point to the ends of the chord.The sum of the squared lengths of any two chords intersecting at right angles at a given point is the same as that of any other two perpendicular chords intersecting at the same point and is given by 8 r 2 − 4 p 2, where r is the circle radius, and p is the distance from the centre point to the point of intersection.

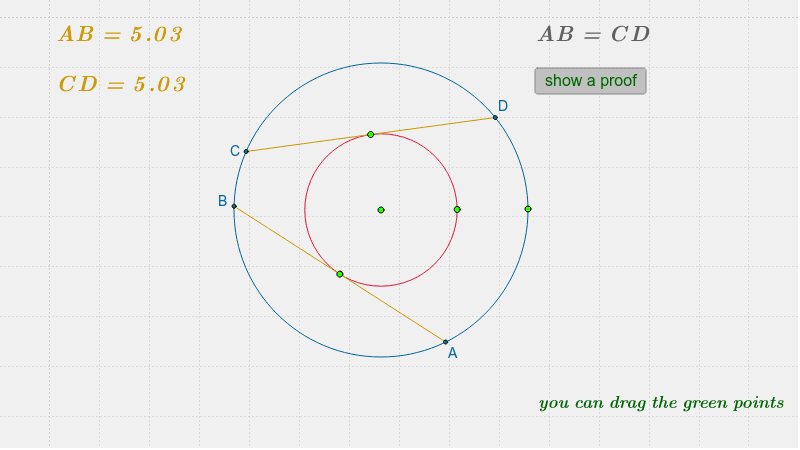
If the intersection of any two perpendicular chords divides one chord into lengths a and b and divides the other chord into lengths c and d, then a 2 + b 2 + c 2 + d 2 equals the square of the diameter.If the intersection of any two chords divides one chord into lengths a and b and divides the other chord into lengths c and d, then ab = cd.Among all the circles with a chord AB in common, the circle with minimal radius is the one with diameter AB.The diameter is the longest chord of the circle.An inscribed angle subtended by a diameter is a right angle (see Thales' theorem).For a cyclic quadrilateral, the exterior angle is equal to the interior opposite angle.If two angles are inscribed on the same chord and on opposite sides of the chord, then they are supplementary.If two angles are inscribed on the same chord and on the same side of the chord, then they are equal.If a central angle and an inscribed angle of a circle are subtended by the same chord and on the same side of the chord, then the central angle is twice the inscribed angle.The line segment through the centre bisecting a chord is perpendicular to the chord.A perpendicular line from the centre of a circle bisects the chord.The perpendicular bisector of a chord passes through the centre of a circle equivalent statements stemming from the uniqueness of the perpendicular bisector are:.Chords are equidistant from the centre of a circle if and only if they are equal in length.In Cartesian coordinates, it is possible to give explicit formulae for the coordinates of the centre of the circle and the radius in terms of the coordinates of the three given points. Through any three points, not all on the same line, there lies a unique circle.Thought of as a great circle of the unit sphere, it becomes the Riemannian circle.The circle that is centred at the origin with radius 1 is called the unit circle.The constants of proportionality are 2 π and π respectively.The area enclosed and the square of its radius are proportional.A circle circumference and radius are proportional.The group of rotations alone is the circle group T.

Its symmetry group is the orthogonal group O(2, R).
This is the largest distance between any two points on the circle.
EQUIDISTANT CHORD GEOMETRY FULL
Specifying two end points of an arc and a centre allows for two arcs that together make up a full circle. Annulus: a ring-shaped object, the region bounded by two concentric circles.


 0 kommentar(er)
0 kommentar(er)
